二叉排序树的介绍和实现
介绍
假设最开始有一个数据集,里面只有一个数{62},接下来要插入88,数据集变成{62,88},继续保持从小到大排序;下面插入58,想要继续有序排列,就要插入到第一个,将,62和88都向后移动一位。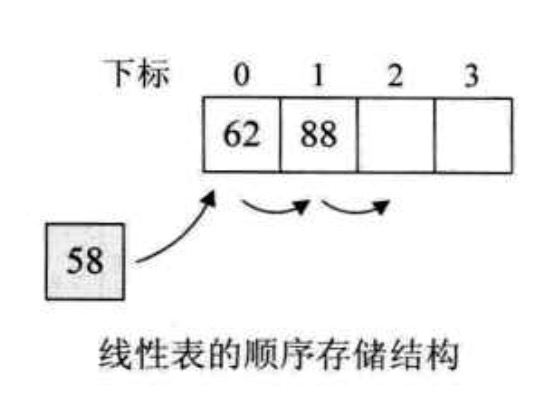
可以看出这样插入的效率有点低。而使用二叉树的方式来插入,则62和88就不需要移动原本的位置,效率会提高很多。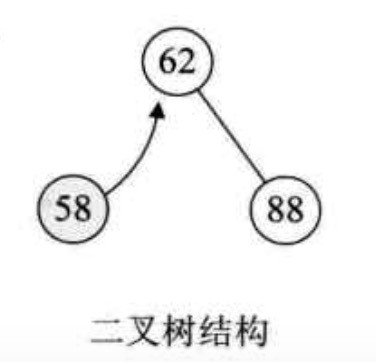
现在要对集合{62,88,58,47,35,73,51,99,37,93}进行查找插入,可以用排好序的二叉树来创建。
先插入62,根结点,88比62大,放入右子树;
58比62小,放入62的左子树;
47比58小,放入58的左子树;
35比47小,放入47的左子树;
73比62大但比88小,放入88的左子树;
51比47大但比58小,放入47的右子树;
99比88大,放入88的右子树;
37比35大但比47小,放入35的右子树;
93比88大但比99小,放入99的左子树。
这种称为二叉排序树。
二叉排序树的实现
结点的定义
1 | class BiNode: |
二叉排序树的查找实现:
1 | class SearchBiTree(BiTree): |
当找到结点是,返回结果True和结点;当没有找到结点时,返回结果False和最后一个不为空的结点。
拿上面的例子来看,当现有的集合为{62,88,58,47,35}时,要插入下一个数73。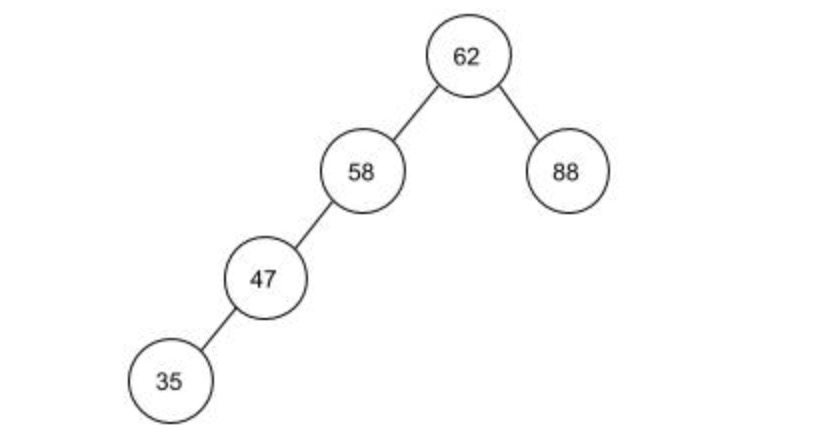
先获取到根结点62,比较73和62,发现73比62大,去62的右子数去继续查找。
62的右子数是88,比较73和88,发现73比88小,就去88的左子数继续查找。
而88的左子数为空,就返回结果False和最后一个不为空的结点88。
这里用到了递归的思想来实现二叉树的查找。
二叉排序树的插入操作
1 | def insert_search_tree(self, num): |
代码很简单,通过查找方法,如果找到,就返回结果False;没找到,就根据最后一个不为空的结点来比较,大于它就插入到右叶子,小于它就插入到左叶子。
二叉排序树的删除操作
对于二叉排序树结点的删除,相比较插入而言,有点复杂。
先写下代码:
1 | def delete_search_tree(self, num): |
代码的优化可能不是那么好,只是写下来基本的逻辑思想。
要删除结点,首先要找到结点,这里的search方法,返回的是目标结点的父结点,这样找的原因是为了方便删除的操作,原因和链表的删除类似。
找到目标结点的父结点后,就可以根据比较判断它是父结点的左孩子还是右孩子。
下面就要进行删除操作,这里分为三种情况。这里来距离说明以下。
要删除的目标结点没有左右孩子结点,这种情况就是直接把结点拿掉就可以了。
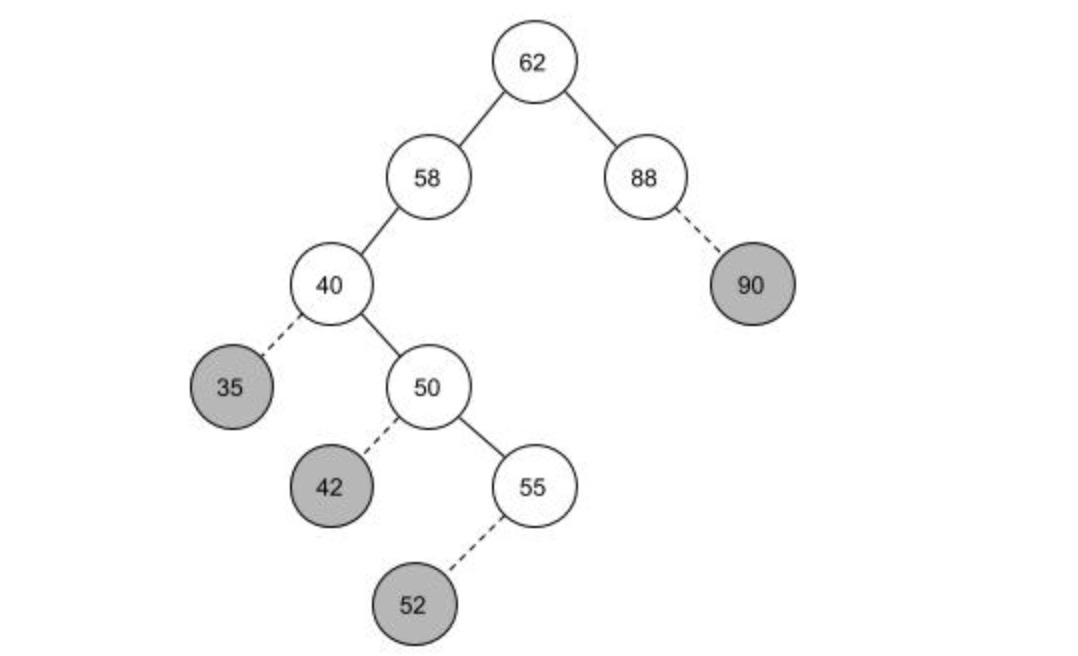 当要拿掉35,42,52,90结点是,直接将这些结点与父结点的关联断开即可,对原有的树结构没有造成影响。
当要拿掉35,42,52,90结点是,直接将这些结点与父结点的关联断开即可,对原有的树结构没有造成影响。
当目标结点只有左孩子或只有右孩子,也相对好操作一点。
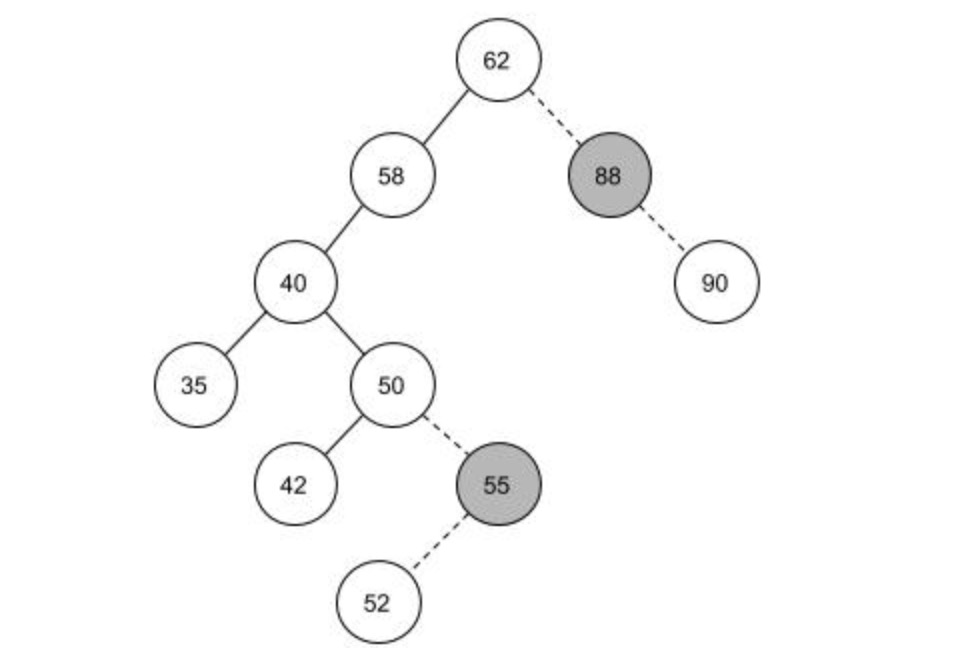 当要删掉55,88结点时,55是它的父结点右孩子,那么将50结点的右孩子指向55的左孩子即可,将55的两个关联断开;对于88结点来说也是一样的原理。
当要删掉55,88结点时,55是它的父结点右孩子,那么将50结点的右孩子指向55的左孩子即可,将55的两个关联断开;对于88结点来说也是一样的原理。
当目标结点既有左孩子又有右孩子,这时的操作就会复杂一点。
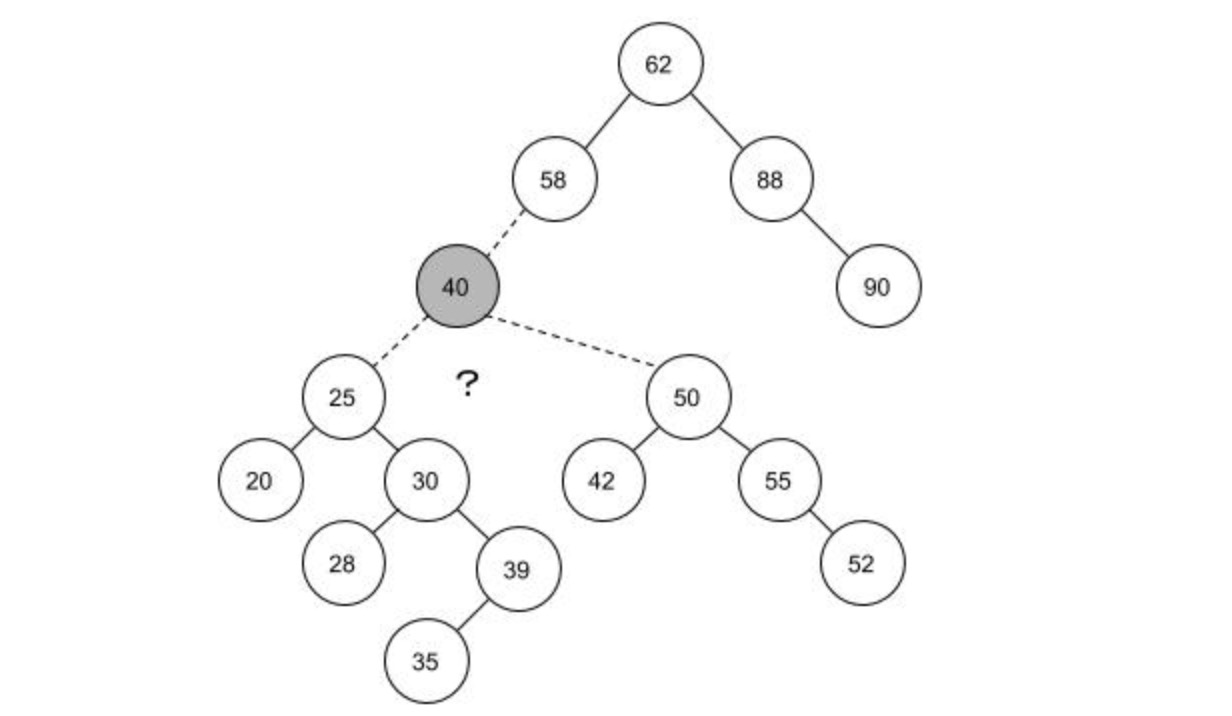 简单粗暴的思路是,将目标结点40的左子树原封不动的挂到结点58下面,然后将40的右子树的每个结点进行插入操作,重新形成一个新树。这样的操作理解方便,但当右子树上的结点很多时,这样的操作效率就会很低;这样也会造成一个后果,就是树的高度会变大,这样会操作不好的结果,这会在下面说明原因。
简单粗暴的思路是,将目标结点40的左子树原封不动的挂到结点58下面,然后将40的右子树的每个结点进行插入操作,重新形成一个新树。这样的操作理解方便,但当右子树上的结点很多时,这样的操作效率就会很低;这样也会造成一个后果,就是树的高度会变大,这样会操作不好的结果,这会在下面说明原因。
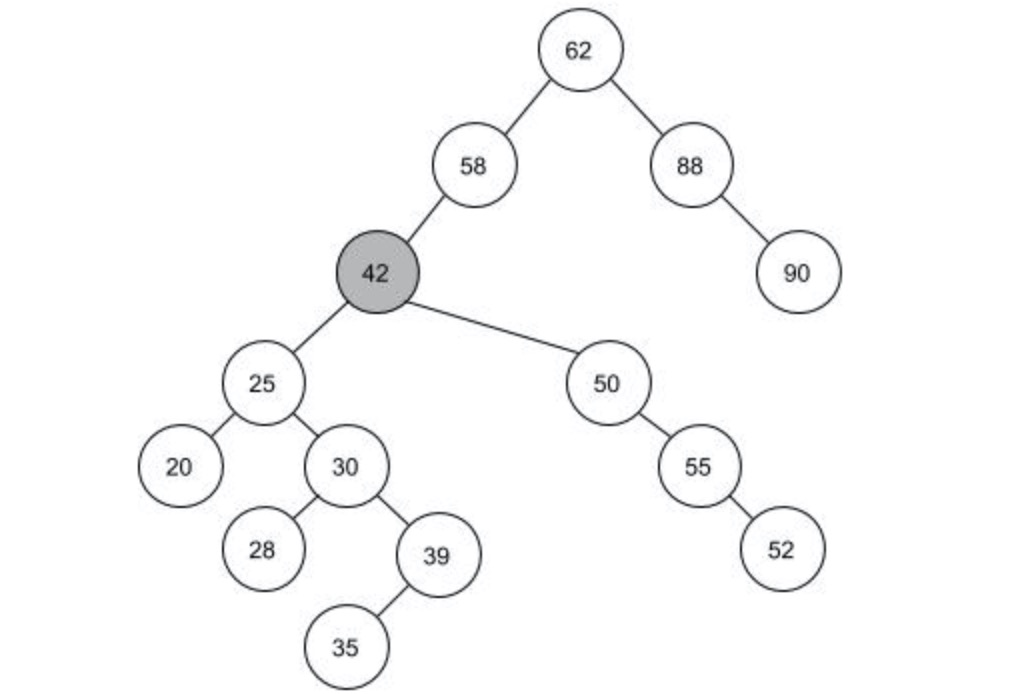
还有一种方法就是找到一个结点将目标结点40替换掉。这样的结点在上图中有两个,结点39和结点42。因为这两个结点的是最接近目标结点的两个结点,用这两个来替换对树的影响最小。我们把这两个结点称为结点40的前驱和后继。左图用前驱结点39来替换,右图用后继结点42来替换。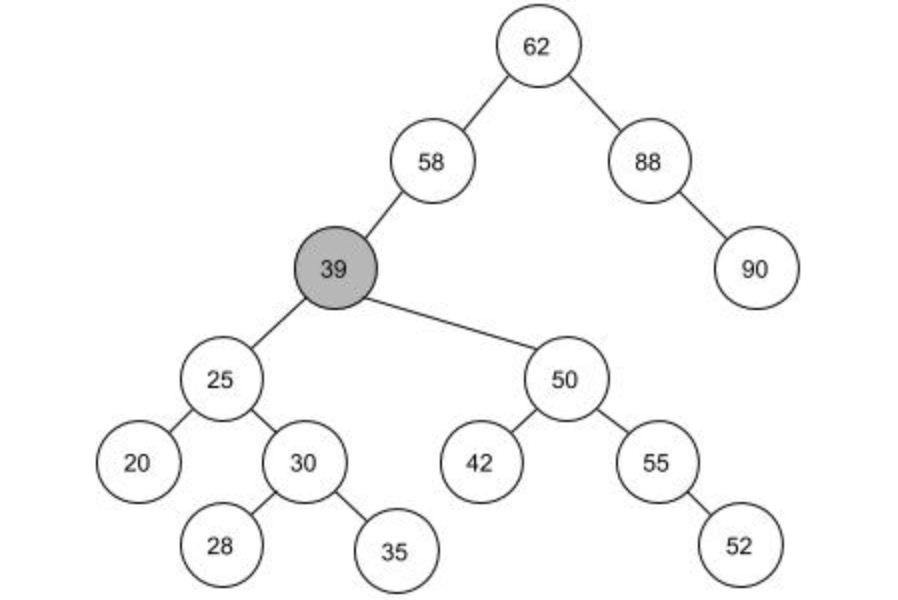
总结
二叉排序树用链接的方式来存储,避免了插入删除操作时的结点整体移动问题,插入删除效率大大提高。
二叉排序树的查找,它的效率取决于目标结点到根结点的层数。层数越高效率越低。
当有这样一个集合{35,37,47,51,58,62,73,88,93,99},下面两种二叉排序树:
当要查找99时,左侧查询两次即可,右侧则要查询10次,效率差别很大。
当二叉排序树比较平衡时,它的效率比较高,时间复杂度趋近于O(logn)。
不平衡的极端情况就是右侧二叉树,它的时间复杂度为O(n),等同于顺序查找,体现不了二叉树的优越性。
因此,当希望用二叉排序树来对一个集合进行查找时,需要构造一个相对平衡的二叉排序树。
完整代码查看:
https://github.com/dougaoyang/struct_code/blob/master/tree/btree_search.py