随机梯度下降算法

以线性回归为例：
预测函数为：
$$ h_\theta(x) = \theta^Tx $$
代价函数：
$$ J_{train}(\theta) = \frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 $$

重复：{
　　$ \theta_j:=\theta_j−\alpha \left( \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} \right) $
}

当数据量过大时，梯度下降的算法会变得很慢，因为要对所有的数据进行求和。因为每次重复梯度下降都是所有数据全部求和，所以梯度下降算法又称之为批量梯度下降（Batch Gradient Descent）

概念说明

随机梯度下降在每一次迭代中，不用考虑全部的样本，只需要考虑一个训练样本。

针对一个样本，它的代价函数：
$$ cost(\theta, (x^{(i)},y^{(i)})) = \frac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2 $$
而针对所有样本的代价函数可以看作是对每个样本代价函数的平均：
$$ J_{train}(\theta) = \frac{1}{m}\sum_{i=1}^m cost(\theta, (x^{(i)},y^{(i)})) $$

随机梯度下降算法如下：
第一步，先随机打乱训练集样本。
第二步，进行梯度下降：
重复 {
　　循环所有样本 for i=1,2,3,…,m {
　　　　$ \theta_j:=\theta_j−\alpha (h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} $
　　}
}

一开始随机打乱数据是为了对样本集的访问是随机的，会让梯度下降的速度快一点。

该算法一次训练一个样本，对它的代价函数进行一小步梯度下降，修改参数$\theta$，使得它对该样本的拟合会好一点；然后再对下一个样本进行运算，直到扫描完所有的训练样本，最后外部在迭代这个过程。

跟批量梯度下降算法不同的是，随机梯度下降不需要等到所有样本求和来得到梯度项，而是在对每个样本就可以求出梯度项，在对每个样本扫描的过程中就已经在优化参数了。

在梯度下降过程中，批量梯度下降的过程趋向于一条直线，直接收敛到全局最小值；而随机梯度下降不太可能收敛到全局最小值，而是随机地在其周围震荡，但通常会很接近最小值。

随机梯度下降通常需要经过1-10次外部循环才能接近全局最小值。

判断收敛

在批量梯度下降中，要判断是否收敛，需要在每一次迭代算法后计算$J_{train}$的值，根据值的变化来判断收敛。
在执行随机梯度下降时，不需要计算所有的样本的代价函数，只用在对某个样本进行梯度下降前计算该样本的代价函数$cost(\theta, (x^{(i)},y^{(i)})) $，为了判断是否收敛，可以计算多次迭代后$cost(\theta, (x^{(i)},y^{(i)})) $的平均值，例如1000次迭代，在每次更新$\theta$前，计算最后1000次的的cost的平均值。

选择每隔多少次计算成本函数对梯度下降的过程也有影响：

上图中蓝色曲线是每1000次迭代，红色的是每隔5000次迭代。
因为随机梯度下降时会出现震荡，当迭代次数少时发现下降的曲线起伏很多，而迭代次数变大时，曲线就会变得平滑许多。缺点是每隔5000个计算，会增加计算成本。

增加迭代次数可以判断算法是否正确：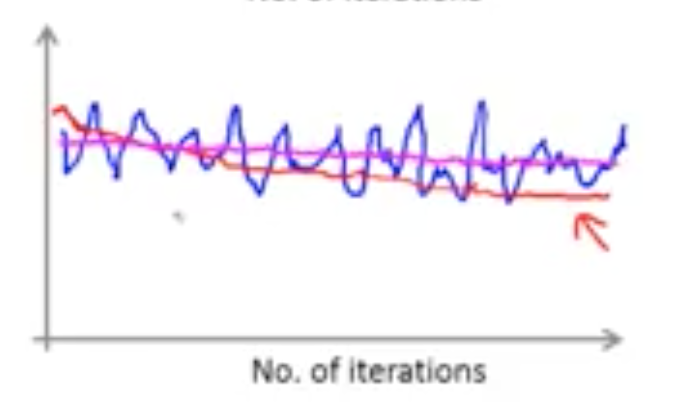

上图蓝色的是1000个迭代次数，通过这条曲线，不能很好的判断成本函数是否在下降，这时就需要添加迭代次数，当增加到5000次，则可以通过平滑的曲线判断，当下滑曲线是红色的时，说明算法是有效的，代价函数值在下降；当是紫色的曲线时，可以看到是一个平坦的线，这时判断算法可能出现问题了。

在随机梯度下降中，学习率$\alpha$也会影响算法，当学习率减小时，下降曲线的震荡就会变小，而且会收敛到一个更好的解：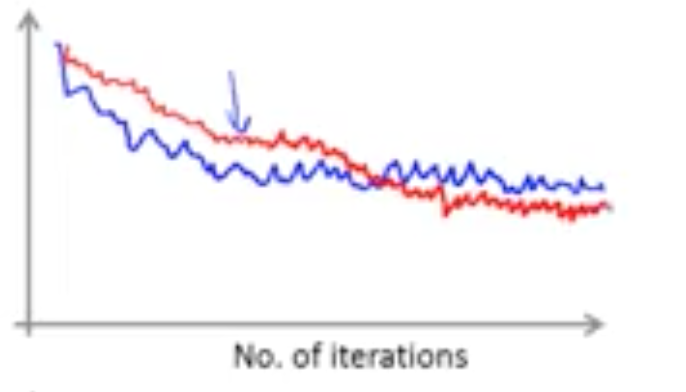

图中红色的曲线时学习率更小的一个，可以看到震荡变小，且下降到一个更小的值。

当看到曲线是上升的时候，可以尝试减小学习率看看效果。

在随机梯度下降中，如果想要收敛到全剧最小值，需要随着时间的变化减小学习率$\alpha$的值：
$$ \alpha = \frac{const1}{iterNumber + const2} $$
学习率等于一个常数除以迭代次数加另一个常数，随着迭代次数增大，学习率会减小；但这会造成常数1和常数2的选择问题。